Equações diferenciais de ordem N
-Metodo dos coeficientes indeterminados
Considere o seguinte PVI(problema de valor inicial):


A equação diferencial do PVI é de 2ºgrau.
Agora vamos colocar-la na forma de polinómio caracteristico.
Considerando que Dy=y', a equação fica com o aspecto:

Se b(t) for da forma :

pode-se usar este metodo de resolução de equações diferenciais(metodo dos coeficientes indeterminadas).Caso contrario, teriamos que usar o metodo da variação das constantes, que é bem mais complicado do que este.
A solução final da equação diferencial é um misto de solução particular e solução homogénea.
Equação diferencial que dará a solução Particular:

Agora vamos encontrar os zeros desta equação e para isso usaremos a formula resolvente.
Verifica-se que os zeros são numeros complexos conjugados:
Zeros:

Sendo assim a equação diferencial homogénea pode-se escrever da seguinte forma:

Solução homogénea:
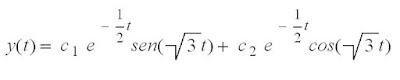
Mas como y(0)=0 e o sen(o)=0, logo c1=0 e por isso a equação homogénea fica com a forma:

De seguida vamos ter de calcular a solução particular. Para isso precisamos de saber qual é o polinomio aniquilador de b(t). O polinomio aniquilador de b(t) não é mais do que um polinomio que anula b(t) para que possamos ter, tal como na determinação da solução homogénea, uma equação diferencial que está igualada a zero.
Em seguida estão os varios polinomios aniquiladores para as varias formas possiveis de b(t)

Agora que sabemos os varios polinomios aniquiladores vamos multiplicar o polinomio aniquilador a ambos os membros da equação diferencial do PVI.

Por exemplo vamos considerar b(t)=t.
Usando as formulas de cima descobrimos que o polinomio aniquilidor de t é :

Assim a equação que dará origem á solução particular é:

As Soluções desta equação são as seguintes:

Se reparmos com atenção vamos perceber que o 3º termo desta equação é igual á solução da equação homogénea. Sendo assim, a solução particular é composta apenas pelos 2 primeiros termos da solução de cima.
Solução Particular:

Em seguida temos de calcular os termos indeterminados da equação particular(c1,c2).
Como a equação diferencial é y''+y'+y=t.
A forma como nós temos para encontrar os coeficientes,c1 e c2,(podiam ser mais coeficientes) é fazer com que a equação particular verifique também ela a igualdade:

No fim do calculo dos coeficientes é só somar a solução particular com a solução homogenea e encontrar, dessa forma, a solução geral.

Nesta solução geral o c1 e c2 são os coeficientes indeterminados que acabaram de ser determinados. O c3 é um coeficiente que vai ser determinado usando as condições iniciais do PVI (Problema de valor inicial), que neste caso é y(o)=0. No final de todos os coeficientes calculados, o problema de valor inicial fica resolvido.
Considere o seguinte PVI(problema de valor inicial):


A equação diferencial do PVI é de 2ºgrau.
Agora vamos colocar-la na forma de polinómio caracteristico.
Considerando que Dy=y', a equação fica com o aspecto:

Se b(t) for da forma :

pode-se usar este metodo de resolução de equações diferenciais(metodo dos coeficientes indeterminadas).Caso contrario, teriamos que usar o metodo da variação das constantes, que é bem mais complicado do que este.
A solução final da equação diferencial é um misto de solução particular e solução homogénea.
Equação diferencial que dará a solução Particular:

Agora vamos encontrar os zeros desta equação e para isso usaremos a formula resolvente.
Verifica-se que os zeros são numeros complexos conjugados:
Zeros:

Sendo assim a equação diferencial homogénea pode-se escrever da seguinte forma:

Solução homogénea:
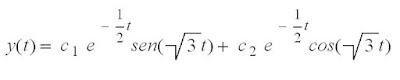
Mas como y(0)=0 e o sen(o)=0, logo c1=0 e por isso a equação homogénea fica com a forma:

De seguida vamos ter de calcular a solução particular. Para isso precisamos de saber qual é o polinomio aniquilador de b(t). O polinomio aniquilador de b(t) não é mais do que um polinomio que anula b(t) para que possamos ter, tal como na determinação da solução homogénea, uma equação diferencial que está igualada a zero.
Em seguida estão os varios polinomios aniquiladores para as varias formas possiveis de b(t)

Agora que sabemos os varios polinomios aniquiladores vamos multiplicar o polinomio aniquilador a ambos os membros da equação diferencial do PVI.

Por exemplo vamos considerar b(t)=t.
Usando as formulas de cima descobrimos que o polinomio aniquilidor de t é :

Assim a equação que dará origem á solução particular é:

As Soluções desta equação são as seguintes:

Se reparmos com atenção vamos perceber que o 3º termo desta equação é igual á solução da equação homogénea. Sendo assim, a solução particular é composta apenas pelos 2 primeiros termos da solução de cima.
Solução Particular:

Em seguida temos de calcular os termos indeterminados da equação particular(c1,c2).
Como a equação diferencial é y''+y'+y=t.
A forma como nós temos para encontrar os coeficientes,c1 e c2,(podiam ser mais coeficientes) é fazer com que a equação particular verifique também ela a igualdade:

No fim do calculo dos coeficientes é só somar a solução particular com a solução homogenea e encontrar, dessa forma, a solução geral.

Nesta solução geral o c1 e c2 são os coeficientes indeterminados que acabaram de ser determinados. O c3 é um coeficiente que vai ser determinado usando as condições iniciais do PVI (Problema de valor inicial), que neste caso é y(o)=0. No final de todos os coeficientes calculados, o problema de valor inicial fica resolvido.
Donwload desta matéria

.png)
